SUBPROGRAMAS

SUBPROGRAMAS 

Mediante el uso de los subprogramas, es posible diseñar sistemas modulares en los cuales ya no existe un solo algoritmo que se encarga de todo, sino que tenemos diferentes algoritmos especializados por temas y que en conjunto forman el gran programa. 

Nuestro propio organismo esta dividido en subprogramas en los cuales cada parte tiene un fin específico e interactúan para mantener todo el sistema en pleno funcionamiento. 

Los sub-programas también se conocen con el nombre de subrutinas, módulos, operaciones o métodos. 

Debemos ver a los subprogramas como una estrategia para dividir un problema mayor en partes más pequeñas, de forma que al interactuar entre ellos el sistema se comporte tal y como se diseñó.

Cada subprograma es en realidad un algoritmo más pequeño que aporta parte de la solución al problema principal. En estos subprogramas podemos definir variables, realizar asignaciones, realizar lectura de datos, imprimir expresiones, variables y literales, usar ciclos, vectores, decisiones, incluso invocar o llamar  a otros subprogramas.

A Pesar de usar todos los subprogramas que se deseen siempre habrá de existir uno denominado principal, el cual es el encargado de organizar el uso de los elementos y subprogramas disponibles. Un programa siempre inicia en su parte principal y es desde allí de donde se articulan los elementos a ser usados.

 

Como funciona un programa que esta estructurado por subprogramas?

El programa inicia en su parte principal, es desde allí donde se ejecuta linea a linea, cuando el programa desea utilizar un subprograma, realiza un llamado,al cual se le conoce con el nombre de invocación. 

En este llamado,es vital conocer el nombre del subprograma que se desea invocar y los elementos que se deben enviar para que éste funcione adecuadamente, el programa ejecuta cada instrucción del subprograma que fue llamado, y cuando termina, regresa retornando el resultado y permitiendo que el programa siga la ejecución en la parte donde había sido llamado.

Los subprogramas tienen dos aspectos claves.

1. Un subprograma se crea una sola vez.

Esto implica hacer el algoritmo que se encuentra en el interior del subprograma de forma que cumpla un fin específico.

2. Un subprograma se usa n veces en un subprograma

Desde cualquier parte del programa se puede llamar a un subprograma creado con el fin de ser usado, solo se necesita enviar los parámetros necesarios para su correcto funcionamiento.

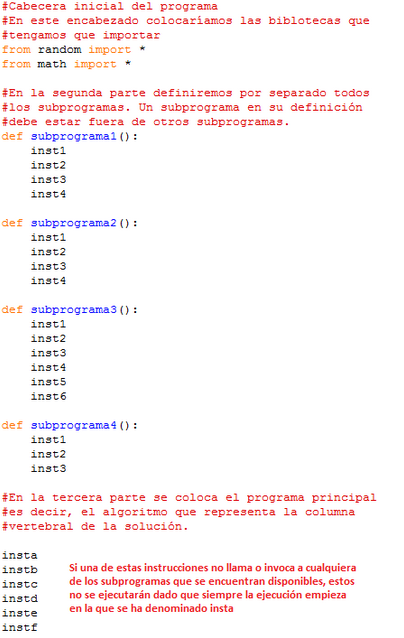
Forma general para definir un subprograma en el lenguaje python.

Para utilizar un subprograma se aplica la misma técnica que trabajamos para las funciones definidas por el sistema.

Para construir un subprograma se necesita:

1. Asignarle un nombre que sea acorde a lo que se espera realice el subprograma

2. Definir el número de parámetros que se necesitarán para su funcionamiento. En este punto la idea es que en un comienzo desde el enunciado se sugiera el número de parámetros que necesitará el subprograma y que más adelante se desarrolle esa habilidad.

3. Crear el algoritmo que se encuentra en el interior del subprograma. Utilizando los parámetros como datos de entrada y aplicando cualquiera de las instrucciones que se venían  aplicando en los algoritmos realizados hasta ahora.

4. Si el programa debe retornar un resultado, este se logra mediante el uso de la instrucción return seguida de lo que se desea retornar. 

Forma general de un programa construido con subprogramas.

1. ¿Para crear un programa con subprogramas siempre hay que importar las bibliotecas?

No. Eso solo depende si se necesitan funciones definidas por el sistema en lo que deseamos construir.

2. ¿Dos subprogramas pueden llamarse igual?

No. Cada subprograma debe tener un único nombre que lo identifique de los demás.

3. ¿Los parámetros pueden llamarse igual?

En un mismo subprograma cada parámetro debe ser diferente de los otros, cada parámetro se separa de los demás por el uso de comas. Pero dos subprogramas si pueden tener el mismo nombre de los parámetros, dado que cada uno es independiente de los demás.

4. ¿Qué instrucciones pueden ir dentro de un subprograma?

Todas las que se han trabajo.

- Definición de variables

- Realización de operaciones lógicas, matemáticas...

- Toma de decisiones if, else, elif ...

- Realización de ciclos, simples y anidados.

- Aplicación de vectores 

- Utilización de funciones definidas por el sistema

- Utilización de subprogramas.

5.¿Puede ejecutarse un subprograma solo?

No. Todo subprograma debe ser llamado desde otra parte del programa y ningún subprograma se ejecutará sin que exista un programa principal que desencadene su utilización.

6. ¿Cuántas veces puedo utilizar un subprograma?

Un subprograma puede ser utilizado las veces que se desee, no hay limites. Pero si se aplica una llamada recursiva, es decir, un programa que se llama a si mismo n veces puede saturar la memoria del computador y bloquear el programa que se esta ejecutando.

7. ¿Que pasa cuando en dos subprogramas se definen variables con el mismo nombre?

Al estar en subprogramas diferentes, no les sucede nada, dado que cada subprograma genera una capsula que la convierte en independiente de los demás e incluso independiente del programa principal.

ARREGLOS BIDIMENSIONALES, UNIDIMENSIONALES, MULTIDIMENSIONALES

ARREGLOS BIDIMENSIONALES 

Este tipo de arreglos al igual que los anteriores es un tipo de dato estructurado, finito ordenado y homogéneo. El acceso a ellos también es en forma directa por medio de un par de índices.

Los arreglos bidimensionales se usan para representar datos que pueden verse como una tabla con filas y columnas. La primera dimensión del arreglo representa las columnas, cada elemento contiene un valor y cada dimensión representa una relación

La representación en memoria se realiza de dos formas : almacenamiento por columnas o por renglones.

Para determinar el número total de elementos en un arreglo bidimensional usaremos las siguientes fórmulas:

RANGO DE RENGLONES (R1) = Ls1 - (Li1+1)

RANGO DE COLUMNAS (R2) = Ls2 - (Li2+1)

No. TOTAL DE COMPONENTES = R1 * R2

REPRESENTACION EN MEMORIA POR COLUMNAS

x : array [1..5,1..7] of integer

Para calcular la dirección de memoria de un elemento se usan la siguiente formula:

A[i,j] = base (A) + [((j - li2) R1 + (i + li1))*w]

REPRESENTACIÓN EN MEMORIA POR RENGLONES

x : array [1..5,1..7] of integer

Para calcular la dirección de memoria de un elemento se usan la siguiente formula:

A[i,j] = base (A) + [((i - li1) R2 + (j + li2))*w]

donde:

i = Indice del renglón a calcular

j = Indice de la columna a calcular

li1 = Límite inferior de renglones

li2 = Límite inferior de columnas

w = Número de bytes tipo componente

VÍDEO:

ARREGLOS UNIDIMENSIONALES 

Un arreglo unidimensional es un tipo de datos estructurado que está formado de una colección finita y ordenada de datos del mismo tipo. Es la estructura natural para modelar listas de elementos iguales.

El tipo de acceso a los arreglos unidimensionales es el acceso directo, es decir, podemos acceder a cualquier elemento del arreglo sin tener que consultar a elementos anteriores o posteriores, esto mediante el uso de un índice para cada elemento del arreglo que nos da su posición relativa.

Para implementar arreglos unidimensionales se debe reservar espacio en memoria, y se debe proporcionar la dirección base del arreglo, la cota superior y la inferior.

REPRESENTACIÓN EN MEMORIA

Los arreglos se representan en memoria de la forma siguiente:

                x : array[1..5] of integer

Para establecer el rango del arreglo (número total de elementos) que componen el arreglo se utiliza la siguiente formula:

                RANGO = Ls - (Li+1)

donde:

ls = Límite superior del arreglo

li = Límite inferior del arreglo

Para calcular la dirección de memoria de un elemento dentro de un arreglo se usa la siguiente formula:

                A[i] = base(A) + [(i-li) * w]

donde :

A = Identificador único del arreglo

i = Indice del elemento

li = Límite inferior

w = Número de bytes tipo componente

Si el arreglo en el cual estamos trabajando tiene un índice numerativo utilizaremos las siguientes fórmulas:

                RANGO = ord (ls) - (ord (li)+1)

                A[i] = base (A) + [ord (i) - ord (li) * w]

VÍDEO:

ARREGLOS MULTIDIMENSIONALES 

Este también es un tipo de dato estructurado, que está compuesto por n dimensiones. Para hacer referencia a cada componente del arreglo es necesario utilizar n índices, uno para cada dimensión

Para determinar el número de elementos en este tipo de arreglos se usan las siguientes fórmulas:

RANGO (Ri) = lsi - (lii + 1)

No. TOTAL DE ELEMENTOS = R1 * R2* R3 * ...* Rn

donde:

i = 1 ... n

n = No. total de dimensiones

Para determinar la dirección de memoria se usa la siguiente formula:

LOC A[i1,i2,i3,...,in] = base(A) + [(i1-li1)*R3*R4*Rn + (i2-li2)*R3*R2*... (in - lin)*Rn]*w

VÍDEO:

 Operaciones Con Arreglos:

Las operaciones en arreglos pueden clasificarse de la siguiente forma:

• Lectura
• Escritura
• Asignación
• Actualización
• Ordenación
• Búsqueda
  
  
  
  

A).    LECTURA

Este proceso consiste en leer un dato de un arreglo y asignar un valor a cada uno de sus componentes.

La lectura se realiza de la siguiente manera:

para i desde 1 hasta N haz

x<--arreglo[i]

B).    ESCRITURA

Consiste en asignarle un valor a cada elemento del arreglo.

La escritura se realiza de la siguiente manera:

para i desde 1 hasta N haz

arreglo[i]<--x

C).    ASIGNACION

No es posible asignar directamente un valor a todo el arreglo, por lo que se realiza de la manera siguiente:

para i desde 1 hasta N haz

arreglo[i]<--algún_valor

D).    ACTUALIZACION

Dentro de esta operación se encuentran las operaciones de eliminar, insertar y modificar datos. Para realizar este tipo de operaciones se debe tomar en cuenta si el arreglo está o no ordenado.

Para arreglos ordenados los algoritmos de inserción, borrado y modificación son los siguientes:

1.- Insertar.

Si i< mensaje(arreglo contrario caso En arreglo[i]<--valor i<--i+1 entonces>

2.- Borrar.

Si N>=1 entonces

inicio

i<--1

encontrado<--falso

mientras i<=n y encontrado=falso

inicio

si arreglo[i]=valor_a_borrar entonces

inicio

encontrado<--verdadero

N<--N-1

para k desde i hasta N haz

arreglo[k]<--arreglo[k-1]

fin

en caso contrario

i<--i+1

fin

fin

Si encontrado=falso entonces

mensaje (valor no encontrado)

3.- Modificar.

Si N>=1 entonces

inicio

i<--1

encontrado<--falso

mientras i<=N y encontrado=false haz

inicio

Si arreglo[i]=valor entonces

arreglo[i]<--valor_nuevo

encontrado<--verdadero

En caso contrario

i<--i+1

fin

fin

CICLOS

PSEUDOCÓDIGO

El pseudocódigo (falso lenguaje, el prefijo pseudo significa falso) es una descripción de alto nivel de un algoritmo que emplea una mezcla de lenguaje natural con algunas convenciones sintácticas propias de lenguajes de programación, como asignaciones, ciclos y condicionales, aunque no está regido por ningún estándar.

 Es utilizado para describir algoritmos en libros y publicaciones científicas, y como producto intermedio durante el desarrollo de un algoritmo, como los diagramas de flujo, aunque presentan una ventaja importante sobre estos, y es que los algoritmos descritos en pseudocódigo requieren menos espacio para representar instrucciones complejas.

EJEMPLO:

Las estructuras de control deciden qué camino hay que segui en función de una condición  son las siguientes:

• ESTRUCTURA SECUENCIAL: consiste en colocar una instrucción tras otra, de manera que se van ejecutando de arriba abajo.
• ESTRUCTURA SELECTIVA O CONDICIONAL (si, si no): permiten ejecutar un conjunto de instrucciones u otras en función de si se cumple o no una condición.
• ESTRUCTURA ITERATIVA O DE REPETICIÓN (mientras, repetir, para): permite repetir una instrucción o grupo de ellas un numero fijo de veces o mientras (o hasta que) una condición sea cierta.

EJEMPLOS:

ESTRUCTURA SECUENCIAL:

Pseudocódigo de un algoritmo que calcule la media de tres números:

El orden en el que se realiza los operaciones es importantes : no puede calcularse la media sin antes haber leído los números.

ESTRUCTURA SELECTIVA O CONDICIONAL:

El formato de esta estructura es el siguiente: 

Es Decir, primero se examina la condición: si resulta verdadero, se ejecutan las acciones asociadas al si, en caso contrario se ejecutan las acciones asociadas al sino.

la instrucción si no no es obligatorio en una estructura condicional(si no queremos hacer nada en caso que la condición sea falsa).

Algoritmo que calcula la media de 3 nº y devuelve su raíz cuadrada:

La estructura condicional permite anidar unas instrucciones en otras. 

Supongamos que queremos calcular la nota media de la siguiente forma: 

• Si teoría >= 5 y practica < 5: media = 0.4 x teoría + 0.6 x práctica

• Si practica >= 5 y teoría < 5: media = 0.6 x teoría + 0.4 x práctica

• En cualquier otro caso se calculara su media normalmente. 

ESTRUCTURA ITERATIVA O DE REPETICIÓN:

Esta estructura presenta una serie de variantes que permiten: 

Estructura mientras.

Esta estructura permite repetir un conjunto de instrucciones 0 o más veces, ya que la condición se verifica antes de entrar en el bucle.

El formato de esta estructura es el siguiente:

Es decir, primero se examina la condición: si resulta falsa, se pasa directamente a la instrucción que haya tras el fin, de manera que nos saltamos todas las instrucciones que haya dentro del bucle. 

Estructura repetir … mientras

Esta estructura evalúa la condición una vez realizada la acción. Por tanto, las instrucciones que están dentro se ejecutan al menos una vez. 

El formato de esta estructura es el siguiente:

Ej: algoritmo que lee por teclado unos números (hasta que introduzcamos un número negativo) y calcula su media.

Ej: Algoritmo anterior usando el repetir

Estructura para:

Permite realizar una acción un número determinado de veces.

El formato de esta estructura es el siguiente: 

En cada iteración del bucle variable va tomando distintos valores comprendidos entre inicio y fin. En la primera iteración toma el valor inicio, en la segunda inicio+1, y así sucesivamente hasta el valor fin. 

Ej: Algoritmo que pide 20 números por teclado y calcula su media. 

Restamos 1 a n ya que se sale del bucle para cuando la variable n sobrepasa el valor 20. 

La estructura para puede sustituirse por mientras o por repetir:

¿Cual de las tres variantes usar ante un determinado problema?: 

Un error muy común con las estructuras de repetición consiste en poner mal la condición de finalización u olvidarse de incrementar el contador, dando lugar a bucles infinitos (bucles que no acaban nunca). 

Ej: Calcular la media de una serie de nº positivos dados por teclado. Un valor de 0, como entrada, indicará el final de la serie de números. 

Ej: Calcular la suma de los N primeros números impares, siendo N un nº dado por teclado.

 vídeos: